Why study elastic mechanisms
Elastic mechanisms can be found across the tree of life and allow organisms to manipulate the power of their movements. Like archers, some organisms use their muscles to load their springs with elastic energy and then rapidly release that energy in an explosive movement with more power than possible with just muscle alone.
The elastic structures in these organisms can take multiple shapes and can be made of completely different materials; yet, they are all still capable of storing and releasing tremendous amounts of elastic energy. By studying elastic mechanisms across many species, we learn the multiple strategies that nature has taken, and we can use that information to inform our understanding of the elastic structures in our bodies and in our machines.
How to study elastic mechanisms
The technology required to measure whether or not an organism uses elastic mechanisms is well-developed. We can calculate the power of movements from high speed videos. There is good evidence for a spring-loaded mechanism if the measured power of movement exceeds the maximum power that muscles can generate. Also, advances in ultrasound and sonomicrometry allow in vivo measurements of stretch and compression (other good indicators of energy storage).
We still, however, require advances in research and technology to understand how these elastic mechanisms work. Once an elastic system is identified, many questions still need to be answered. What biological parameters determine how much energy is stored and recovered? Is the stiffness of the system tuned for a particular movement? How can organisms modulate the mechanics of their systems to produce movements in different contexts? Do the multiple structures that comprise the mechanism interact with each other?
To address these questions, I use a combination of mechanical testing and computer simulation. By using machines designed for engineering and materials science, I measure the physical response of biological materials to stretching and/or compression. I then incorporate these data into computer models developed from first principals of physics. These computer models form new tools that can simulate the effect of experimental manipulations. With these tools, we can test hypothetical situations (e.g., what is the effect of increasing spring stiffness) while remaining firmly grounded in the laws of physics and the variation of physical parameters observed in biological systems.
Recent work
Are tendons tuned to muscle activation dynamics?
The duration of muscle activation can affect the maximum force the muscle can generate; shorter durations of muscle activation can lead to lower muscle force. Muscle force, in conjunction with spring stiffness, determines the amount of stored elastic energy in the system. In this project, we compared the springs of bullfrogs (which activate their muscles for a short duration before movement) with those of grasshoppers (which activate their muscle for a long duration before movement) and asked whether spring stiffness was tuned to maximize energy storage in both systems.
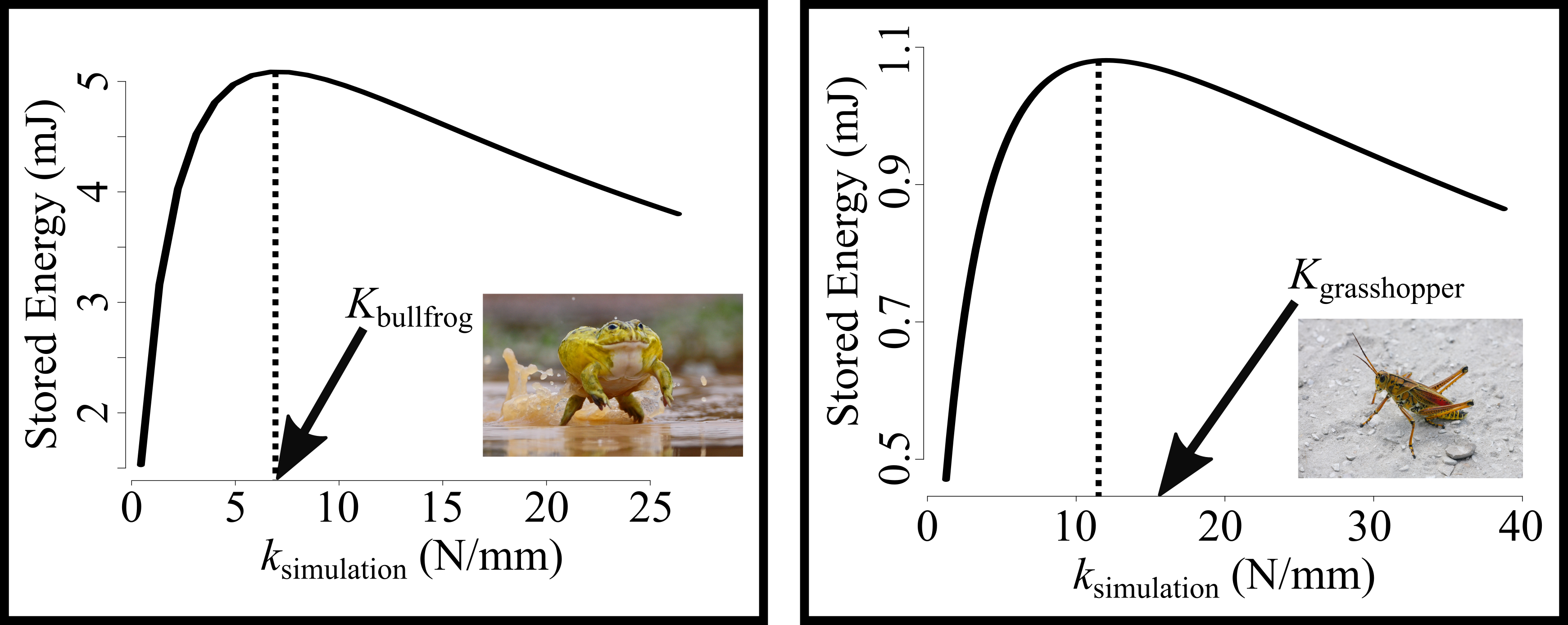
We tested this by simulating variation in spring stiffness (ksimulation) and calculating how much energy was stored in the spring by a virtual muscle, which was activated for a short duration in the bullfrog simulations and for a long duration in the grasshopper simulations. The simulations showed that there is an optimal spring stiffness in bullfrogs and grasshoppers (dotted line), and we found that the actual spring stiffness values for these animals (arrows) are very close to the optimal values. This suggests that the spring stiffness is tuned for short and long durations of muscle activation in bullfrogs and grasshoppers, respectively.
Are tendon fascicles sensitive to fast stress-rates?
To some extent, nearly all biological materials behave viscoelastically; they reversibly store energy when deformed (elasticity) but are also affected by how fast the deformation occurs (viscosity). In collagenous tissues such as tendons and intervertebral cartilage, this effect has been studied at long timescales on the order of 100 - 1000 seconds. But, few studies have characterized this effect at the timescales of muscle activation (0.050 - 0.250 seconds). Because muscle activation can cause deformation of tendons, it is important to characterize viscoelasticity at these relatively fast rates and small timescales.
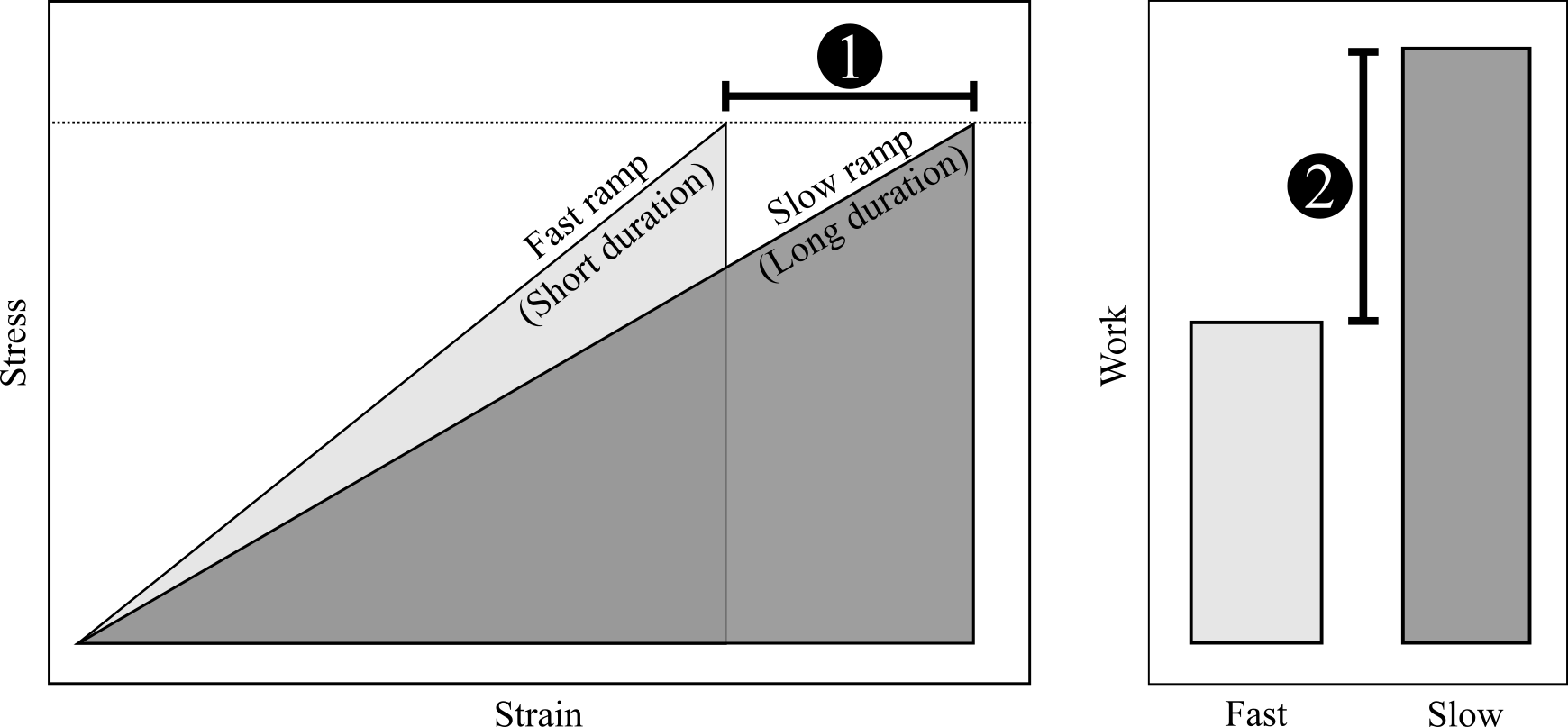
Generally, the faster the rate, the stiffer the mechanical response (slope of stress-strain curve). That means that for a given amount of muscle stress (horizontal dotted line), a faster rate of stress will produce less strain than a slower rate (1). This may also lead to a difference in work or stored elastic energy (2; area under each stress-strain curve). In this study, we applied different rates of stress to many tendon fascicles to determine whether or not their mechanical behaviors vary at these fast stress-rates and small timescales.
What is the role of tendons in energy dissipation?
When falling from a certain height, the mass of the organism must be slowed to a stop by its musculoskeletal system. Previous work has suggested that tendons play a crucial role in this dissipation of kinetic energy. Although the tendons themselves do not dissipate a significant amount of energy, their hypothesized role is to quickly transform the kinetic energy into elastic energy that can later be dissipated by the muscle at much slower rates, potentially reducing the maximum force and power that the muscle experiences. In this way, the tendon acts as a mechanical buffer.
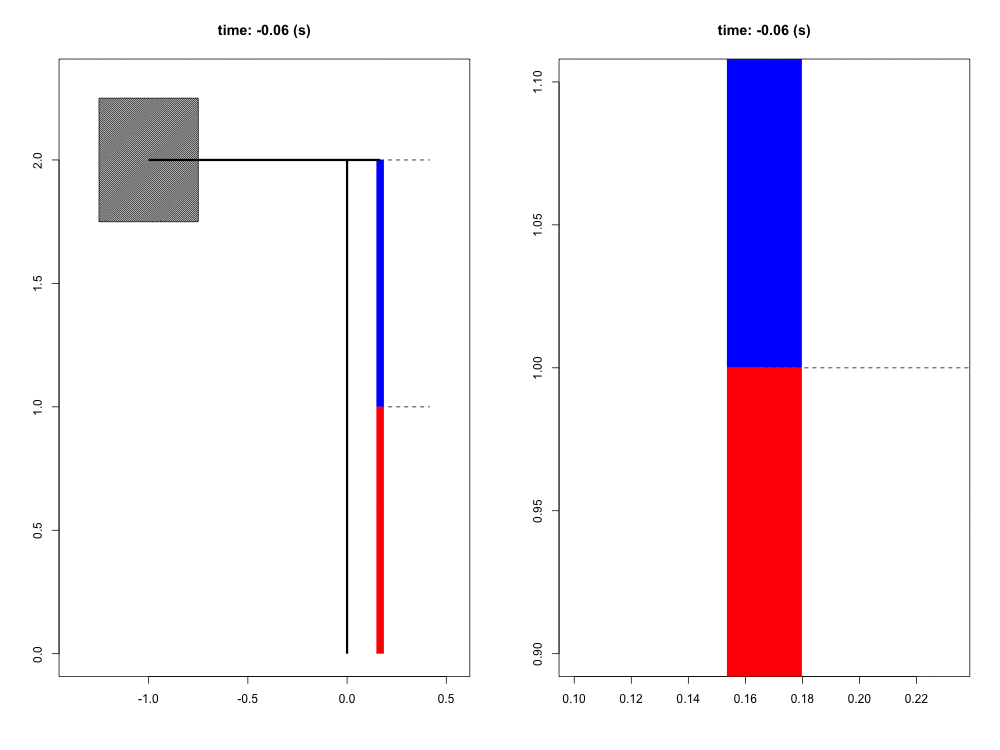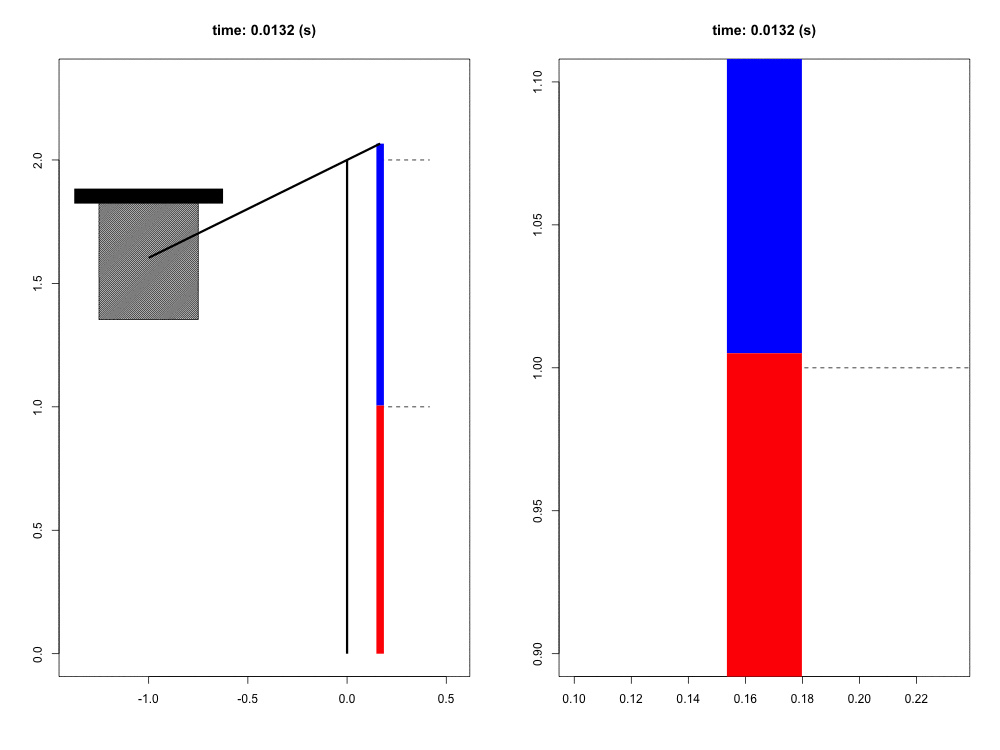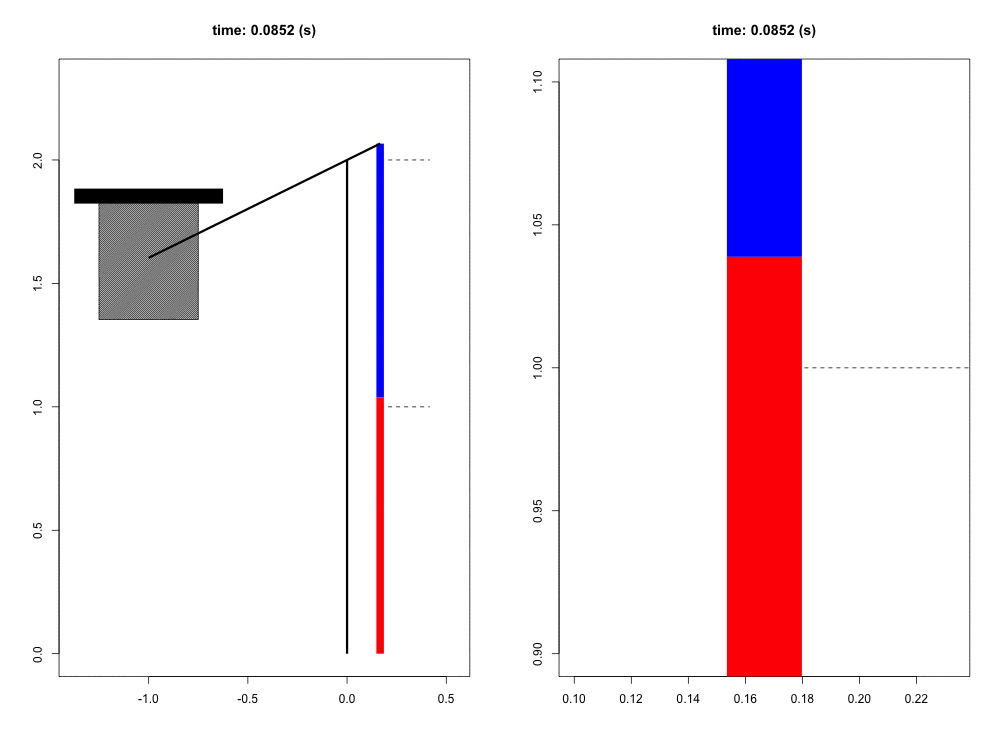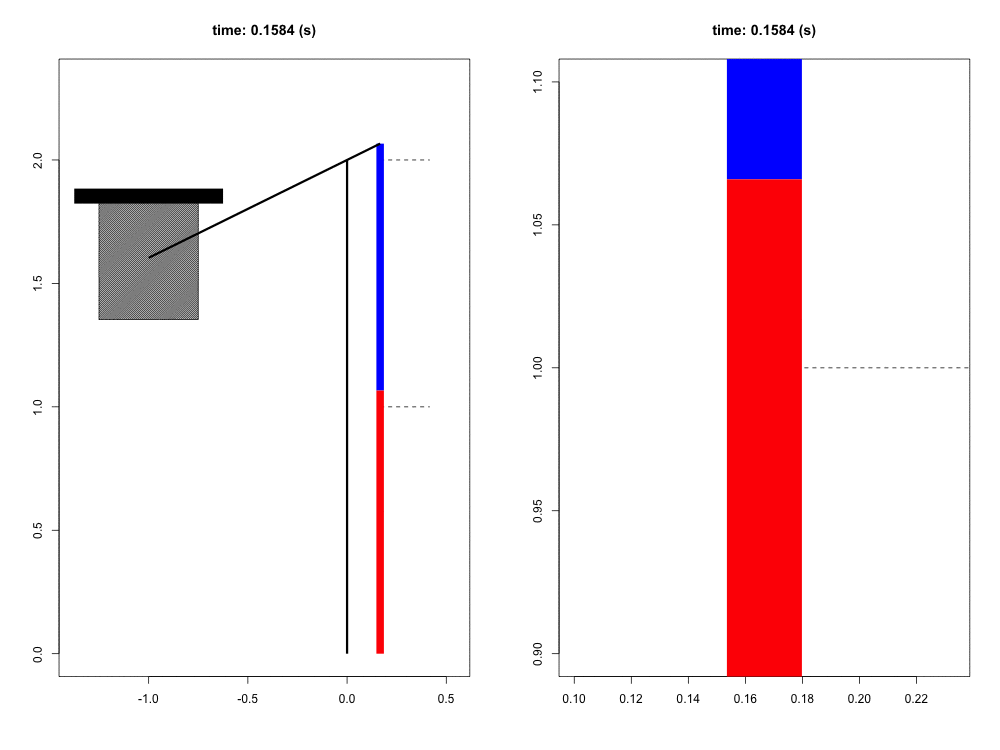
For this project, we have developed a computer simulation of a muscle-tendon system connected to a falling mass. Given what we know about muscle physiology and activation dynamics, we can simulate the interaction of muscle (red) and tendon (blue) that occurs during energy dissipation. The power of this mathematical model is twofold. First, we are able to zoom in and focus on the interaction between muscle and spring (right view) with full control of spatial and temporal scales. Second, this simulation provides a unique opportunity to test the functional role of the tendon simply by comparing these results to those in which the tendon is a completely rigid connection with infinite stiffness. This model also allows us to probe the limits and sensitivity of the system in ways more difficult to do experimentally.